Decision making plays a key role virtually in every aspect of human life such as buying a house or choosing a career. It is the process of selecting a course of action from available options so that the desired result or predetermined objective may be accomplished. However, when decision making is about the future, uncertainty and risk become involved. For instance, how much should one save for retirement given the uncertainty involving such variables as future income and longevity? What is the expected return on different investment choices given the risks? In economics, utility is a measure of how much benefit consumers derive from certain goods or services. From a finance standpoint, it refers to how much benefit investors obtain from portfolio performance considering risk.
It is assumed that an individual, when making a decision in the face of incomplete knowledge, will choose to act in a manner that will result in the highest expected utility with respect to the individual’s subjective probability. This is the expected utility theory that was first introduced by Swiss mathematician Daniel Bernoulli and was later expanded upon in the 20th century by the mathematician John von Neumann and the economist Oskar Morgenstern.
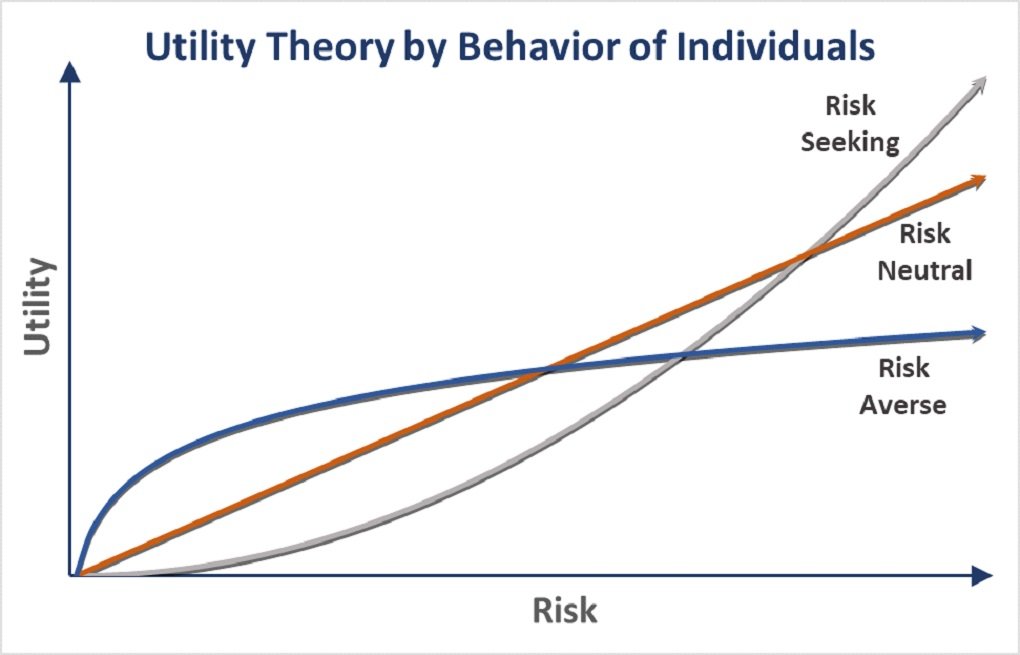
There are three types of individual behaviors that the von Neumann–Morgenstern expected utility function can be used to explain: risk-averse, risk-neutral, and risk-seeking. For example, consider an individual deciding to invest in one of two portfolio strategies, Strategy A or Strategy B. Suppose that Strategy A has a 5% chance of producing $80, a 90% chance of producing $100, and a 5% chance of producing $120. Thus, the expected payoff from Strategy A would be calculated as follows:
Expected Payout for Strategy A: 5% x $80 + 90% x $100 + 5% x $120 = $100
Now suppose Strategy B has the same payoffs but the respective probabilities for the payoffs change to 40%, 20%, and 40%. It is easy to verify that the expected payoff is still $100:
Expected Payout for Strategy B: 40% x $80 + 20% x $100 + 40% x $120 = $100
In other words, mathematically speaking, nothing has changed. The only difference is that the probabilities of the lowest and highest payoffs rose at the expense of the middle one. This means there is more variance (or risk) associated with the possible payoffs. Despite the strategies being mathematically equivalent, the investor may not see them as equal. If she values both investment options equally, she is considered risk neutral. The implication is that she equally values a payoff of $100 with any set of probabilistic payoffs whose expected value is also $100. If she prefers Strategy A over Strategy B, she places higher value on less variability in payoffs. In that regard, by preferring more certainty, she is considered risk averse. Finally, if she actually prefers the increase in variability, she is considered risk-seeking. In a gambling context, a risk averter puts higher utility on the expected value of the gamble than on taking the gamble itself. Conversely, a risk-seeker prefers to take the gamble rather than settle for a payoff equal to the expected value of that gamble.
The implication of the expected utility theory is that individuals seek to maximize the expectation of utility rather than monetary values alone. Since utility functions are subjective, different people can approach any given risky event with quite different valuations. Having a solid understanding of one’s utility of money can help investors make investment decisions that are best suited to their risk attitudes and investment strategies.